第十三届蓝桥杯省赛第一场 C/C++ B 组题解

蓝桥杯

字数统计: 2.8k阅读时长: 11 min

 2022/04/22 

九进制转十进制

送分题，推荐使用 std::stoi 函数，自带进制转换

顺子日期

题面写的很差，对“顺子”没有一个准确的定义（逆序是否算顺子？包括 \(0\) 的是否算顺子？）

若顺子定义为：“从小到大连续三个大于等于 \(0\) 的数字”，则本题做法如下：

首先我们发现年份部分 \(2022\) 是无用的，因为其内部不存在顺子，且最后一位也无法作为顺子的一部分（不存在 \(34\) 月），故我们只看月日部分即可。

若顺子位置在前 \(3\) 位，则：

月份为 \(01\)，那么日期可以为 \(20 \sim 29\)，共 \(10\) 个；
月份为 \(12\)，那么日期可以为 \(30\) 或 \(31\)，共 \(2\) 个。

若顺子位置在后 \(3\) 位，则：

日期为 \(12\)，那么月份可以为 \(10\)，共 \(1\) 个；
日期为 \(23\)，那么月份可以为 \(01\) 或 \(11\)，共 \(2\) 个。

注意在以上过程中我们计算了 \(0123\) 两次，故最终结果为 \(10+2+1+2-1=14\)

刷题统计

按照题意模拟即可

修剪灌木

当一棵灌木被修剪后其高度会变为 \(0\)，而下次再次碰到此灌木时其高度达到最高

故对于中点左侧的灌木来说，其最大高度为其右侧灌木数量乘 \(2\)；对于中点右侧的灌木来说，其最大高度为其左侧灌木数量乘 \(2\)。

X 进制减法

题面解释

首先我们解释一下题面里的 \(321\) 转换后为什么是 \(65\)

设一个 \(X\) 进制数字 \(P\) 每位的数字为 \(p_1,p_2,\cdots,p_n\)，即 \(P = \overline{p_{1}p_{2} \cdots p_{n}}\)，每位的进制为 \(x_1,x_2,\cdots,x_n\)

则其十进制值为 \(p_1(x_{2}x_{3} \cdots x_{n}) + p_2(x_{3}x_{4} \cdots x_{n}) + \cdots + p_n\)

即：

\[P = \sum_{i=1}^{n} \left( p_i \prod_{j=i+1}^{n}x_j \right)\]

故 \((321)_X = 3 \times (10 \times 2) + 2 \times 2 + 1 = 65\)

解题

设 \(A\) 每位的数字为 \(a_1,a_2,\cdots,a_n\)，\(B\) 每位的数字为 \(b_1,b_2,\cdots,b_m~(m \leq n)\)。

若 \(m<n\)，为了方便，我们在 \(B\) 数字前面补前导 \(0\)，使得其长度与 \(A\) 一样。则 \(B\) 每位的数字为 \(b_1,b_2,\cdots,b_n\)。

设每位的进制为 \(x_1,x_2,\cdots,x_n\)，则：

\[ \begin{aligned} A-B &= \sum_{i=1}^{n} \left( a_i \prod_{j=i+1}^{n}x_j \right) - \sum_{i=1}^{n} \left( b_i \prod_{j=i+1}^{n}x_j \right) \\ &= \sum_{i=1}^{n} \left( (a_i-b_i) \prod_{j=i+1}^{n}x_j \right) \end{aligned} \]

在 \(a_i\) 与 \(b_i\) 都给定的情况下，可以发现当 \(\prod_{j=i+1}^{n}x_j\) 越小时，\(A-B\) 越小，也就是每位的进制都取到最小值时，\(A-B\) 最小

注意题面的规定“最低为二进制”与“每一数位上的数字要小于其进制”，故每位的进制最小只能取到 \(\max(2, a_i+1, b_i+1)\)

统计子矩阵

首先有一个很显然的二维前缀和暴力，但时间复杂度为 \(O(n^4)\)，对于 \(500\) 的数据范围显然无法接受

我们发现，子矩阵是连续的，故本题其实即双指针算法维护区间信息的模板题的二维版本

双指针算法维护区间信息的模板题：LeetCode 713 给定一个正整数数组 \(nums\) 和整数 \(k\) 。请找出该数组内乘积小于 \(k\) 的连续的子数组的个数。

在一维数组中使用双指针时，两个指针指向的是零维的点，那么在二维数组中使用双指针时，双指针自然指向的就是一维的线

于是我们只需要遍历这两根一维的线，扫双指针即可。而两线之间元素的和的维护可以使用前缀和轻松解决

一个循环遍历两线的左边界，一个循环遍历两线的右边界，一个循环在限定的左右边界范围内在纵方向扫双指针，时间复杂度 \(O(n^3)\)

积木画

洛谷原题：覆盖墙壁

发现问题要求方案数，而求方案数的题目一般就是两种做法：组合数学或者动态规划。本题显然不像是可以用组合数学解决的，考虑动态规划

以下提供两种动态规划的方法

线性 DP

朴素递推

状态设计：\(dp[i]\) 代表前 \(i\) 列都被填满时的方案数
初始状态：\(dp[0] = 1\)
转移方程：
- 若最后一个放的是竖条
  - \(dp[i-1]+\) 第 \(i\) 列放一个竖条 \(=dp[i]\)
    
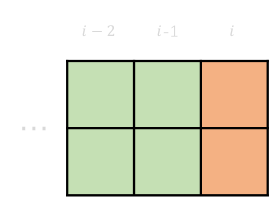
    1-1
  - \(dp[i-2]+\) 第 \(i-1\) 与第 \(i\) 列放两个横条 \(=dp[i]\)
    
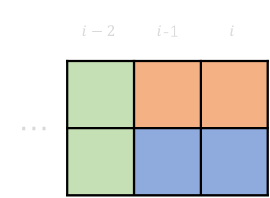
    1-2
- 若最后一个放的是 L 条，最后一个放的 L 条有两种放法，故答案乘 \(2\)
  - \(dp[i-3]+\) 放两个 L 条 \(=dp[i]\)
    
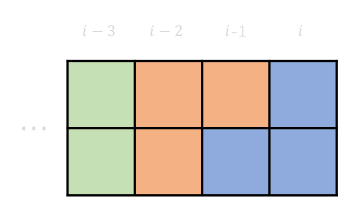
    1-3
  - \(dp[i-4]+\) 两个 L 条一个横条 \(=dp[i]\)
    
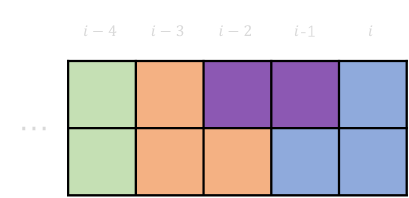
    1-4
  - \(dp[i-5]+\) 两个 L 条两个横条 \(=dp[i]\)
    
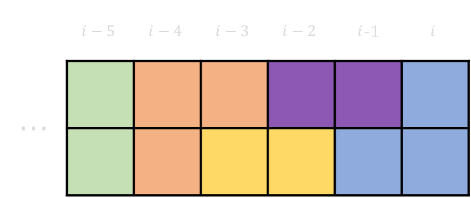
    1-5
  - \(\vdots\)
即：

\[ \begin{aligned} dp[i] &= dp[i-1]+dp[i-2]+2\sum_{j=0}^{i-3}dp[j] \\ &= dp[i-1]+\left( dp[i-2]+dp[i-3]+2\sum_{j=0}^{i-4}dp[j] \right)+dp[i-3] \\ &= 2dp[i-1] + dp[i-3] \end{aligned} \]
所求结果：\(dp[n]\)

可以滚动数组优化

矩阵加速

显然以上转移方程可以矩阵加速：

\[ \begin{cases} 2 \times dp[i-1] + 0 \times dp[i-2] + 1 \times dp[i-3] = dp[i] \\ 1 \times dp[i-1] + 0 \times dp[i-2] + 0 \times dp[i-3] = dp[i-1] \\ 0 \times dp[i-1] + 1 \times dp[i-2] + 0 \times dp[i-3] = dp[i-2] \end{cases} \Rightarrow \begin{bmatrix} 2 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} dp[i-1] \\ dp[i-2] \\ dp[i-3] \end{bmatrix} = \begin{bmatrix} dp[i] \\ dp[i-1] \\ dp[i-2] \end{bmatrix} \]

当 \(n>3\) 时：

\[ \begin{bmatrix} dp[i] \\ dp[i-1] \\ dp[i-2] \end{bmatrix} = \begin{bmatrix} 2 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}^{n-3} \begin{bmatrix} dp[3] \\ dp[2] \\ dp[1] \end{bmatrix} = \begin{bmatrix} 2 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}^{n-3} \begin{bmatrix} 5 \\ 2 \\ 1 \end{bmatrix} \]

状压 DP

\(j=(0,1)\) 代表第一行是否被填充，\(k=(0,1)\) 代表第二行是否被填充

状态设计：\(dp[i][j][k]\) 代表前 \(i-1\) 列已经填满，第 \(i\) 列的填法为 \((j,k)\) 时的方案数
初始状态：\(dp[1][0][0] = 1\)
转移方程：若第 \(i\) 列没被填满，我们向第 \(i\) 列上放置积木将其填满，而在这个填充的过程中可能会影响到第 \(i+1\) 列：
- \(dp[i][0][0] \rightarrow dp[i+1][0][0]\)
  
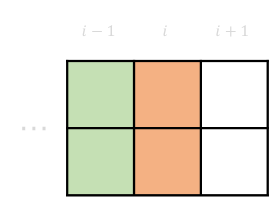
  2-1
- \(dp[i][0][0] \rightarrow dp[i+1][1][1]\)
  
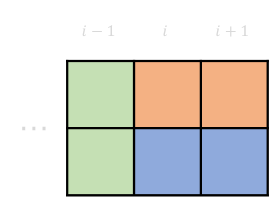
  2-2
- \(dp[i][0][0] \rightarrow dp[i+1][0][1]\)
  
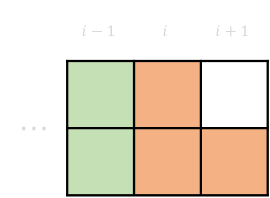
  2-3
- \(dp[i][0][0] \rightarrow dp[i+1][1][0]\)
  
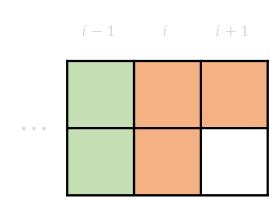
  2-4
- \(dp[i][0][1] \rightarrow dp[i+1][1][0]\)
  
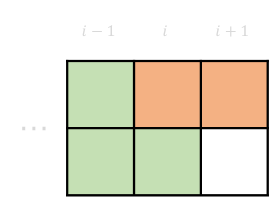
  2-5
- \(dp[i][0][1] \rightarrow dp[i+1][1][1]\)
  
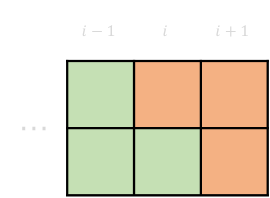
  2-6
- \(dp[i][1][0] \rightarrow dp[i+1][0][1]\)
  
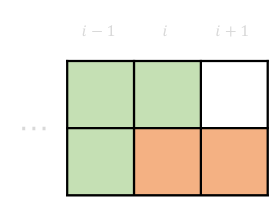
  2-7
- \(dp[i][1][0] \rightarrow dp[i+1][1][1]\)
  
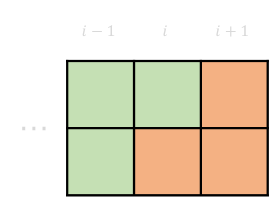
  2-8
- \(dp[i][1][1] \rightarrow dp[i+1][0][0]\)
  
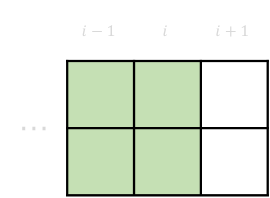
  2-9
所求结果：\(dp[n+1][0][0]\)

每列状态只与上一列有关，故可以滚动数组优化

扫雷

乍一看很像 [NOIP2017 提高组] 奶酪，但一看数据范围发现 \(O(n^2)\) 的时间复杂度过 \(5 \times {10}^4\) 有点悬

但是注意到 \(r\) 最大只有 \(10\)，故对于一个结点我们可以枚举 \(r\) 来获取其能炸到的位置，所以直接搜索就是了。需要注意的是 \(x,y \leq {10}^9\)，我们不能用二维数组存地图，需要使用哈希表 std::unordered_map。另外，std::pair 没有哈希，需要我们自己写一个哈希函数，方法是特化仿函数 std::hash

李白打酒加强版

又是求方案数，一看又不太可能是组合数学，于是 DP。总共就三个变量：店、花、酒的数量，状态设计很简单：

状态设计：\(dp[i][j][k]\) 代表李白遇到了 \(i\) 个店，\(j\) 个花，手上还剩 \(k\) 壶酒的方案数
初始状态：\(dp[0][0][2] = 1\)
转移方程：\(dp[i][j][k] = dp[i-1][j][\frac{k}{2}]+dp[i][j-1][k+1]\)

注意：
1. 只有 \(i \neq 0\) 且 \(2|k\) 时才计算 \(dp[i-1][j][\frac{k}{2}]\) 这个状态
2. 只有 \(j \neq 0\) 时才计算 \(dp[i][j-1][k+1]\) 这个状态
3. \(k\) 这一维度只需要遍历到 \(m-j\) 就足够了，因为每遇到一个花只会喝掉一壶酒，若当前酒的数量大于剩余花的数量则即使之后遇到的都是花酒都喝不完，对最后的答案没有贡献
所求结果：\(dp[n][m-1][1]\)

注意不是 \(dp[n][m][0]\)，因为这样就包含了最后一个单位是店的状态，与题目要求矛盾